No, not a boring relationship, hm, well, sort of. It’s a relationship between two variables such that as one changes in a given direction, the other always changes in the same direction (either in the same direction as the first variable or consistently in the opposite direction).
Details #
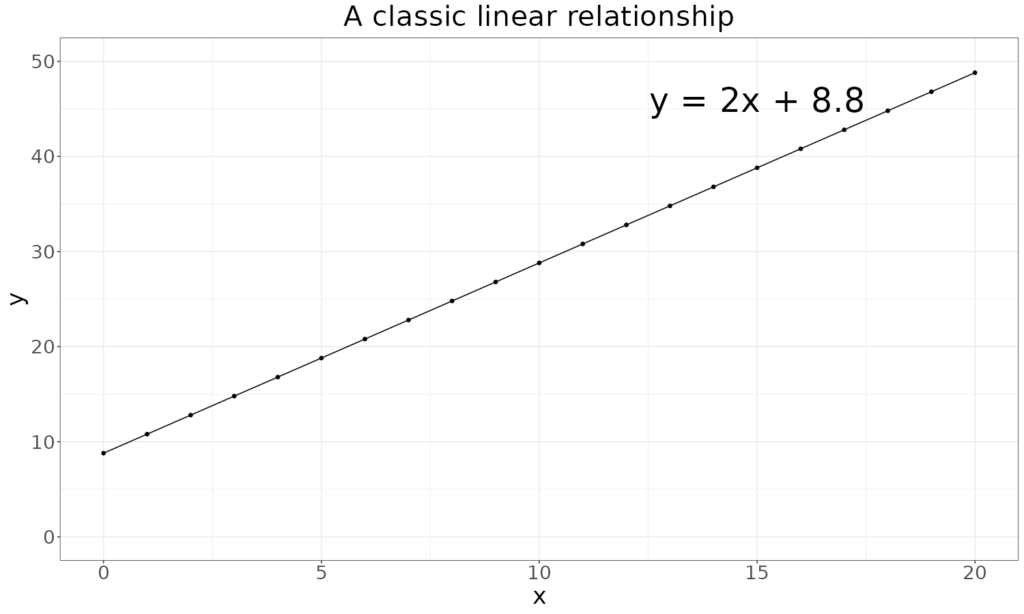
The term is a bit esoteric but the idea is a moderately useful one. Any linear relationship is monotonic. A linear relationship can be written as an equation:
y=mx+cThat says that y is the sum of a constant, c and a multiple, m, of the x value. So if m is positive y will always increase as x increases, a monotonic ascending relationship; if m is negative y will always decrease as x increase, a monotonic descending relationship.
As well as relationships that can be expressed in formulae or equations there are relationships that can be expressed as processes but not as equations. One set of such relationships. One classic of this realm of relationships is that of a “random walk”. Here is a simple random walk where the next value of y is the last value plus a small random addition (between .01 and .2 in this example). This creates a monotonic ascending/increasing relationship.
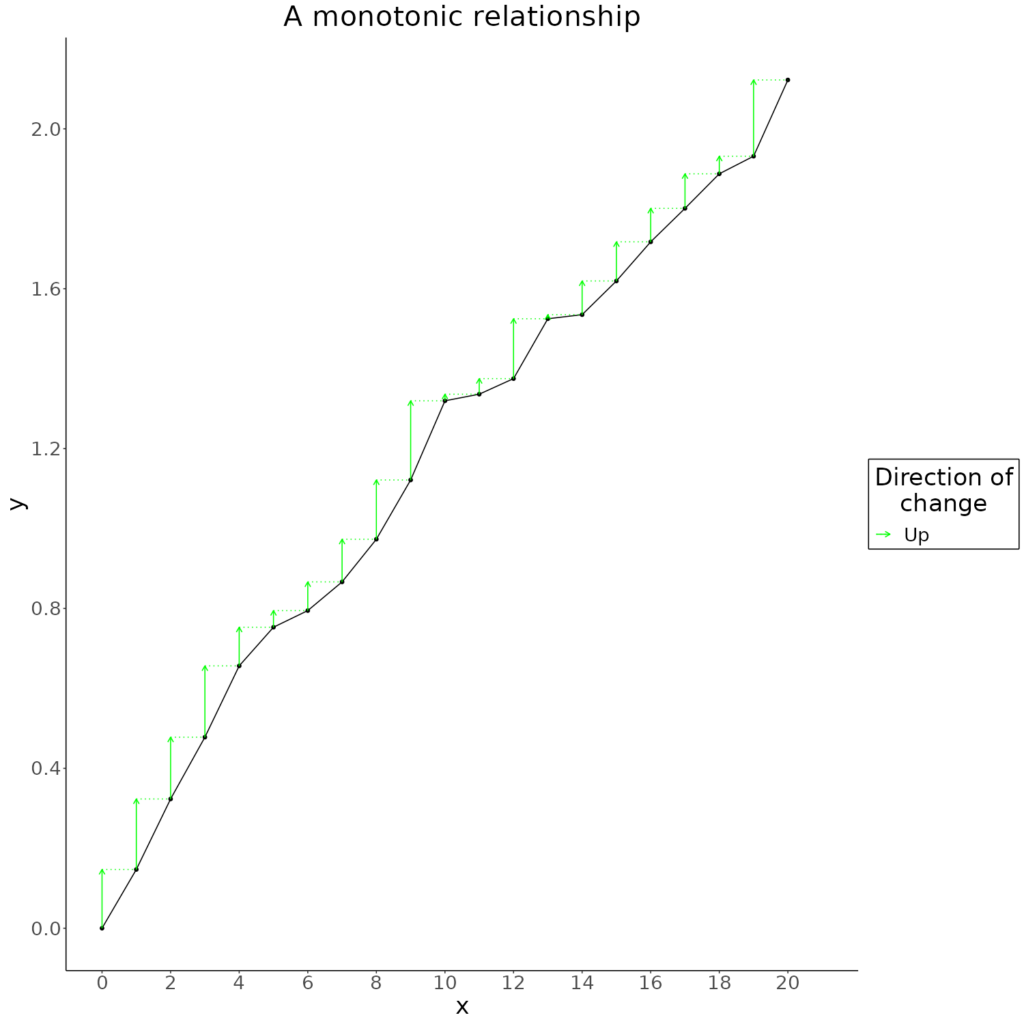
The green arrows there show the random increases in y and they are all positive (as they must fall between .01 and .2 set in the little R program that generated that dataset). It’s easy to tweak that program to generate a non-monotonic random walk.
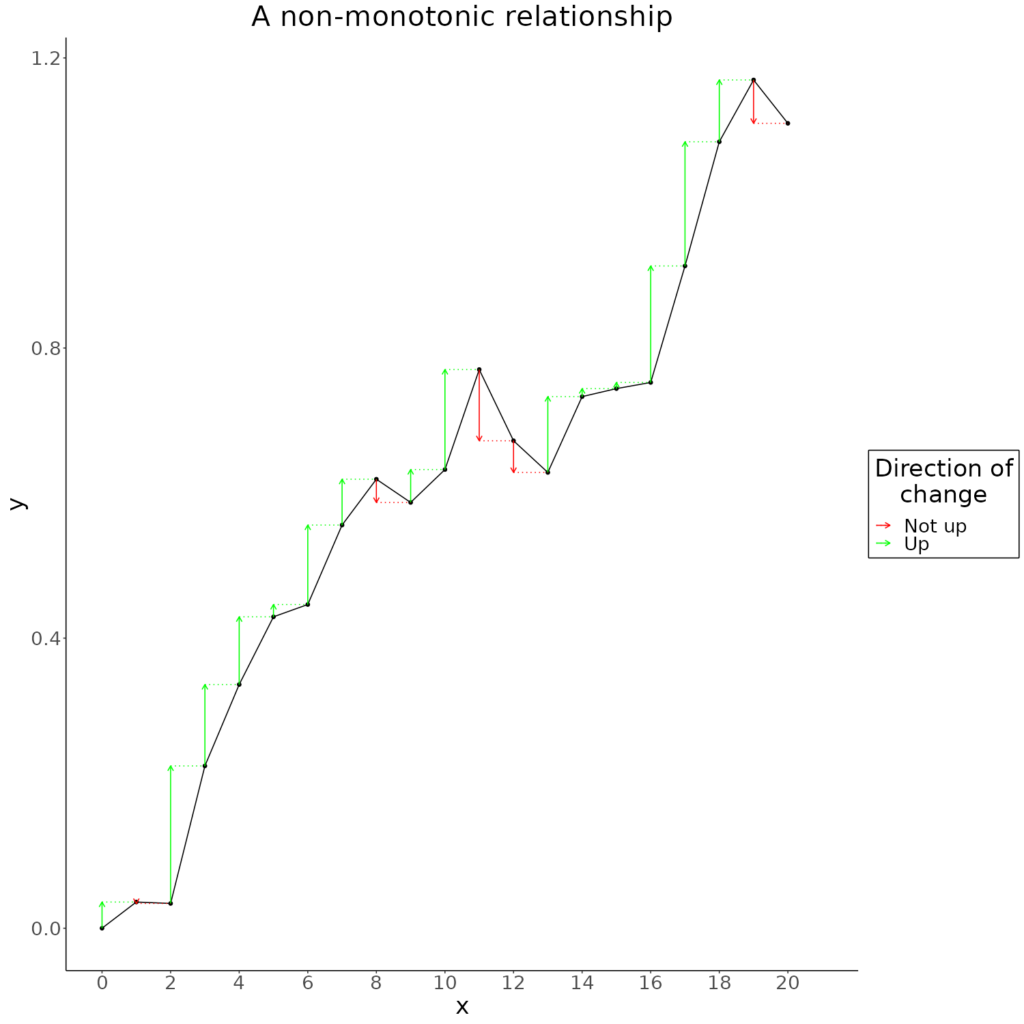
That was created by adding random increments between -.1 and +.2.
Does this really matter?! #
Actually it’s not completely esoteric. One, actually still pretty geeky aspect of this is that monotonic relationships allow perfect ranking, i.e. ranking with no ties and that means that statistical analyses based on ranking apply neatly to monotonic relationships. However, that was more important before computer power exploded and alternative statistical methods for data that aren’t Gaussian in distribution, primarily the bootstrap methods, arrived with the new computer power (i.e. from roughly the 1980s).
More importantly this takes us into the whole area of therapy research which tries to find models of change against time, perhaps a bit of a holy grail game of early 21st Century therapy research!
Try also #
Confidence intervals
Linear versus non-linear processes/relationships
Modelling
Power relationships (mathematical/statistical)
Random numbers
Ranking
Regression and linear regression
Stochastic (processes)
Ties
Transforms/transforming data
Chapters #
Not in the book, just adding a potentially puzzling phrase.
Online resources #
None
Dates #
First created 22.xii.23.

