A square root of a number is the number which multiplied by itself results in the original number, so the square root of 4 is 2, the square root of 9 is 3, of 16 is 4 etc.
This comes up mostly in the relationship between variance and standard deviation as the standard deviation is the square root of the variance.
Details #
The mathematical symbol for a square root is a symbol a bit like a tick mark so \sqrt{9}=3. I remember asking my late uncle what the symbol was seeing it in one of his engineering books. He said, rather haughtily, that it was a square root but I was none the wiser as we hadn’t yet come to that in school maths. I think I was 13 or 14 but that experience has clearly stuck with me!!
The square root of 1 is 1, i.e. in algebra \sqrt{1}=1. The square root of a number larger than one is always smaller than the number, e.g. \sqrt{4}=2, \sqrt{9}=3 etc. That’s shown here.
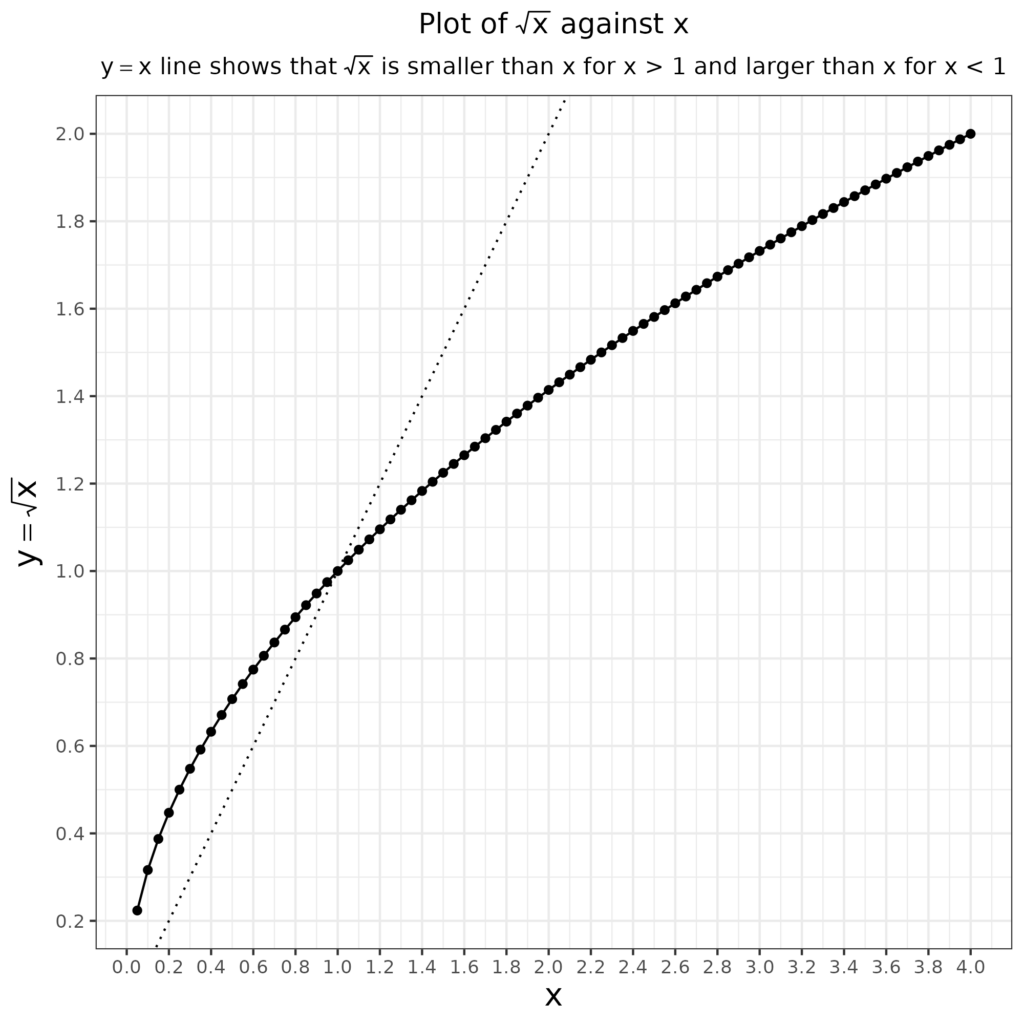
The square root of a positive number smaller than one is larger than the number so \sqrt{\frac{1}{4}}=\frac{1}{2}. The square root of a negative number is impossible as squaring a negative number e.g. -2*-2 = +4 just as squaring a positive number results in a positive number, e.g. 2*2 = 4.
Strictly speaking there are two square roots of any number because two identical numbers multiplied together result in a positive number so -2*-2 = 4 just as 2*2 = 4 so strictly there are two square roots of 4: \sqrt{4}=2 and \sqrt{4}=-2, or \sqrt{4}=\pm2.
Tangential #
Actually, to mathematicians the square root of a negative number does exist but it’s an “imaginary number” so \sqrt{-9}=3i where i is the square root of -1. That was a bit of a shock doing what was then “A level maths” at 17 but it did, as it has for generations of real mathematicians, then come to seem simple and rather wonderful. I hasten to say that I’m not a real mathematician! However, I think it made thinking about the psychoanalytic unconscious much easier to have had that exposure to imaginary numbers (a year or two before I discovered Freud!)
Try also #
Complex numbers
Imaginary numbers
Standard deviation (SD)
Variance
Chapters #
Not really addressed in the book.
Online resources #
Not yet.
Dates #
First created 12.iii.24.

